
In this three-part series of posts, we will discuss a simple machine learning algorithm called Principal Component Analysis (PCA), which can be explained using only knowledge of linear algebra. This algorithm is considered simple and easy to understand, since the reader only requires basic knowledge in one sub field of mathematics. This topic will be divided into three chapters, they are designed to be read independently. So the reader can decide to read the entire series of posts, or read individual chapters depending on the reader’s needs/background. Please note that the reader is assumed to have at least a high school level of mathematical knowledge for understanding any of the above three posts. The three chapters are as follows:
- Chapter 1: Understanding Principal Component Analysis. This post is written for readers who have little to no knowledge of linear algebra.
- Chapter 2: The Actual Workings of PCA. This post is written for readers for readers with knowledge in linear algebra. It rigorously explains two different mathematical methods that power PCA: the Power Iteration Method, and the Singular Vector Decomposition (SVD).
- Chapter 3: Eigenfaces using PCA. This post is written for readers with some programming experience. The chapter will discuss the eigenfaces technique that uses PCA, and will explain a code example written in python.
But of course, to understand the full picture and understand every nuke and cranny of the PCA algorithm, it is advised that the reader starts off from chapter 1 and work their way up to chapter 3.
. . .
2 The Actual Workings of PCA
The definition of the PCA method is, for a given data set and parameter ![]() , to compute the orthonormal
, to compute the orthonormal ![]() -dimensional subspace (through the origin) that minimizes the average squared distance between the points and the subspace, or equivalently that maximizes the variance of the projections of the data points onto the subspace whose basis are called the top
-dimensional subspace (through the origin) that minimizes the average squared distance between the points and the subspace, or equivalently that maximizes the variance of the projections of the data points onto the subspace whose basis are called the top ![]() principal components.
principal components.
In this section we will look at how to actually compute those top ![]() principal components using two different methods:
principal components using two different methods:
- The Power Iteration method.
- The Singular Value Decomposition (SVD) method.
But first, let’s look at what the top ![]() principal components actually are.
principal components actually are.
2.1 Characterizing the Principal Components
2.1.1 The Setup
The PCA method takes in ![]()
![]() -dimensional data points
-dimensional data points ![]() and a parameter
and a parameter ![]() – which is the number of the top principal components desired. We assume that the data is centered around the origin, meaning that
– which is the number of the top principal components desired. We assume that the data is centered around the origin, meaning that ![]() where
where ![]() is the all-zero vector. This can be enforced by subtracting the sample mean
is the all-zero vector. This can be enforced by subtracting the sample mean ![]() from every data point while preprocessing (preparing) the data. The output of the PCA method is defined as
from every data point while preprocessing (preparing) the data. The output of the PCA method is defined as ![]() orthonormal vectors
orthonormal vectors ![]() – the “top
– the “top ![]() principal components” – that maximize the objective function
principal components” – that maximize the objective function
(1) 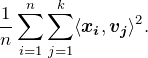
Recall that the inner product ![]() is the projection of
is the projection of ![]() onto
onto ![]() .
.
But how would one actually solve this optimization problem and compute the ![]() ’s? Even with
’s? Even with ![]() , there is an infinite number of unit vectors to try. We’re going to try to build a geometric intuition so that the solution would seem straightforward in hindsight.
, there is an infinite number of unit vectors to try. We’re going to try to build a geometric intuition so that the solution would seem straightforward in hindsight.
2.1.2 Rewriting the Problem
First, let’s consider the ![]() case, which we will later see that the case of general
case, which we will later see that the case of general ![]() reduces to it. With
reduces to it. With ![]() the objective function is
the objective function is
(2) 
To rewrite this variance-maximization in (8) using linear algebra, first we take the data points ![]() and write them as the rows of an
and write them as the rows of an ![]() matrix
matrix ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \[ \boldsymbol{X}=\left[ {\begin{array}{ccc} \boldsymbol{-} & \boldsymbol{x_1} & \boldsymbol{-} \\ \boldsymbol{-} & \boldsymbol{x_2} & \boldsymbol{-} \\ & . & \\ & . & \\ & . & \\ \boldsymbol{-} & \boldsymbol{x_n} & \boldsymbol{-} \\ \end{array} } \right]. \]](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-1d9c70e8cbd5b91e751f0c0a89a9b42b_l3.png)
Thus, for a unit vector ![]() we have
we have
![Rendered by QuickLaTeX.com \[ \boldsymbol{Xv}=\left[ {\begin{array}{c} \langle \boldsymbol{x_1},\boldsymbol{v} \rangle \\ \langle \boldsymbol{x_2},\boldsymbol{v} \rangle \\ . \\ . \\ . \\ \langle \boldsymbol{x_n},\boldsymbol{v} \rangle \\ \end{array} } \right], \]](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-796d06ce79d83b6cc22e72afd20fe51d_l3.png)
so ![]() is just a column vector populated with all the projection lengths of the
is just a column vector populated with all the projection lengths of the ![]() ’s onto the line spanned by
’s onto the line spanned by ![]() . Recall that from (8), we care about the squares of these inner products, which can be obtained by taking the inner product of
. Recall that from (8), we care about the squares of these inner products, which can be obtained by taking the inner product of ![]() with itself:
with itself:
![Rendered by QuickLaTeX.com \[ \boldsymbol{v}^T\boldsymbol{X}^T\boldsymbol{Xv}=(\boldsymbol{Xv})^T\boldsymbol{Xv}=\sum_{i=1}^n\langle \boldsymbol{x_i},\boldsymbol{v} \rangle ^2. \]](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-9ccdacfea19831185bdc0f20be4af1e8_l3.png)
And so, our variance-maximization problem can be rephrased as
(3) ![]()
where ![]() is a
is a ![]() matrix of the form
matrix of the form ![]() . This problem is called “maximizing a quadratic form”. Do note that we are ignoring the
. This problem is called “maximizing a quadratic form”. Do note that we are ignoring the ![]() in (8) because the optimal solution
in (8) because the optimal solution ![]() is the same with or without it.
is the same with or without it.
The matrix ![]() has a natural interpretation. The
has a natural interpretation. The ![]() entry of this matrix is the inner product of the
entry of this matrix is the inner product of the ![]() th row of
th row of ![]() and the
and the ![]() th column of
th column of ![]() – i.e. of the
– i.e. of the ![]() th and
th and ![]() th columns of
th columns of ![]() . So
. So ![]() just collects the inner products of columns of
just collects the inner products of columns of ![]() , and is a symmetric matrix.
, and is a symmetric matrix.
For example, suppose the data points ![]() ’s represent documents, with dimensions (i.e. columns of
’s represent documents, with dimensions (i.e. columns of ![]() ) corresponding to words. Then the inner product of two columns of
) corresponding to words. Then the inner product of two columns of ![]() measures how frequently the corresponding pair of words co-occur in a document. So after centering such an
measures how frequently the corresponding pair of words co-occur in a document. So after centering such an ![]() , frequently co-occurring pairs of words correspond to positive entries of
, frequently co-occurring pairs of words correspond to positive entries of ![]() and pairs of words that almost never appear together are negative entries. The matrix
and pairs of words that almost never appear together are negative entries. The matrix ![]() is called the covariance or correlation matrix of the
is called the covariance or correlation matrix of the ![]() ’s, depending on whether or not each of the coordinates was normalized so as to have unit variance in a preprocessing step.
’s, depending on whether or not each of the coordinates was normalized so as to have unit variance in a preprocessing step.
2.1.3 Solving for the Diagonal Matrices Case
To gain some understanding for the optimization problem in (3) that PCA solves, let’s begin with a very special case: where A is a diagonal matrix
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ {\begin{array}{ccccc} \lambda_1 & & & & 0 \\ & \lambda_2 & & & \\ & & \ddots & & \\ 0 & & & & \lambda_d \end{array} } \right] \end{equation*}](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-ab41c663c2f6992cd0a7521e5d45f318_l3.png)
with sorted nonnegative entries ![]() on the diagonal.
on the diagonal.
There is a simple geometric way to think about diagonal matrices. A ![]() matrix maps points in
matrix maps points in ![]() back to points in
back to points in ![]() – the matrix “moves
– the matrix “moves ![]() around”, in effect. For example, the matrix
around”, in effect. For example, the matrix
![]()
moves each point ![]() of the plane to the point
of the plane to the point ![]() with double the
with double the ![]() -coordinate and the same
-coordinate and the same ![]() -coordinate. For example, the points of the circle
-coordinate. For example, the points of the circle ![]() are mapped to the points
are mapped to the points ![]() of the ellipse shown in Figure 5.
of the ellipse shown in Figure 5.

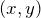 on the unit circle is mapped to
on the unit circle is mapped to 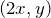 .
. More generally, a diagonal matrix of the form (10) can be thought of as “stretching” ![]() , with the
, with the ![]() th axis getting stretched by the factor
th axis getting stretched by the factor ![]() , and the unit circle being mapped to the corresponding “ellipsoid” (i.e. the analog of an ellipse in more than 2 dimensions).
, and the unit circle being mapped to the corresponding “ellipsoid” (i.e. the analog of an ellipse in more than 2 dimensions).
A natural guess for the direction ![]() that maximizes
that maximizes ![]() with
with ![]() diagonal is the “direction of maximum stretch”, namely
diagonal is the “direction of maximum stretch”, namely ![]() , where
, where ![]() denotes the first standard basis vector (keep in mind that
denotes the first standard basis vector (keep in mind that ![]() ). To verify the guess, let
). To verify the guess, let ![]() be an arbitrary unit vector, and write
be an arbitrary unit vector, and write
(5) ![Rendered by QuickLaTeX.com \begin{equation*} \boldsymbol{v}^T(\boldsymbol{Av})= \left[ {\begin{array}{cccc} v_1 & v_2 & \dotsb & v_d \end{array} } \right] . \left[ {\begin{array}{c} \lambda_1v_1 \\ \lambda_2v_2 \\ \vdots \\ \lambda_dv_d \end{array} } \right] = \sum_{i=1}^d v_i^2\lambda_i . \end{equation*}](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-abef5acbed2c6c18c0922a9695c356d0_l3.png)
Since ![]() is a unit vector, the
is a unit vector, the ![]() ’s sum to 1. Thus
’s sum to 1. Thus ![]() is always an average of the
is always an average of the ![]() ’s, with the averaging weights given by the
’s, with the averaging weights given by the ![]() ’s. Since
’s. Since ![]() is the biggest
is the biggest ![]() , the way to make this average as large as possible is to set
, the way to make this average as large as possible is to set ![]() and
and ![]() for
for ![]() . That is,
. That is, ![]() maximizes
maximizes ![]() , as per our guess.
, as per our guess.
2.1.4 Diagonals in Disguise
Let’s generalize our solution in Section 2.1.3 by considering matrices ![]() that, while not diagonal, are really just “diagonals in disguise.” Geometrically, what we mean is that
that, while not diagonal, are really just “diagonals in disguise.” Geometrically, what we mean is that ![]() still does nothing other than stretch out different orthogonal axes, possibly with these axes being a “rotated version” of the original ones. See Figure 6 for a rotated version of the previous example, which corresponds to the matrix
still does nothing other than stretch out different orthogonal axes, possibly with these axes being a “rotated version” of the original ones. See Figure 6 for a rotated version of the previous example, which corresponds to the matrix
(6) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ {\begin{array}{cc} \frac{3}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{3}{2} \end{array} } \right] = \left[ {\begin{array}{cc} \frac{3}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{3}{\sqrt{2}} \end{array} } \right] . \left[ {\begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} } \right] . \left[ {\begin{array}{cc} \frac{3}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{3}{\sqrt{2}} \end{array} } \right] \end{equation*}](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-fcb2d63a5c6cf4d091c00419cbf6bb77_l3.png)

So what’s a “rotated diagonal” in higher dimensions? The appropriate generalization of a rotation is an orthogonal matrix. Note that orthogonal matrices also capture operations like reflections and permutations of the coordinates. Recall that an orthogonal matrix ![]() is a square matrix where the columns are a set of orthonormal vectors – that is, each column has unit length, and the inner product of two different columns is 0. A key property of orthogonal matrices is that they preserve length – that is,
is a square matrix where the columns are a set of orthonormal vectors – that is, each column has unit length, and the inner product of two different columns is 0. A key property of orthogonal matrices is that they preserve length – that is, ![]() for every vector
for every vector ![]() . We review briefly why this is: since the columns of
. We review briefly why this is: since the columns of ![]() are orthonormal vectors, we have
are orthonormal vectors, we have
(7) ![]()
since the ![]() entry of
entry of ![]() is just the inner product of the
is just the inner product of the ![]() th and
th and ![]() th columns of
th columns of ![]() (It also follows that
(It also follows that ![]() . This shows that
. This shows that ![]() is also an orthogonal matrix, or equivalently that the rows of an orthogonal matrix are orthonormal vectors). This means that the inverse of an orthogonal matrix is simply its transpose. Example (12) is a good representation for this. Then, we have
is also an orthogonal matrix, or equivalently that the rows of an orthogonal matrix are orthonormal vectors). This means that the inverse of an orthogonal matrix is simply its transpose. Example (12) is a good representation for this. Then, we have
![]()
showing that ![]() and
and ![]() have same norm.
have same norm.
Now consider a matrix ![]() that can be written as
that can be written as ![]() for an orthogonal matrix
for an orthogonal matrix ![]() and diagonal matrix
and diagonal matrix ![]() as in (10) – this is what we mean by a “diagonal in disguise”. Such a matrix
as in (10) – this is what we mean by a “diagonal in disguise”. Such a matrix ![]() has a “direction of maximum stretch” – the (rotated) axis that gets stretched the most (i.e. by
has a “direction of maximum stretch” – the (rotated) axis that gets stretched the most (i.e. by ![]() ). Since the direction of maximum stretch under
). Since the direction of maximum stretch under ![]() is
is ![]() , the direction of maximum stretch under
, the direction of maximum stretch under ![]() is the direction that gets mapped to
is the direction that gets mapped to ![]() under
under ![]() – which is
– which is ![]() or, equivalently,
or, equivalently, ![]() . Notice that
. Notice that ![]() is simply the first column of
is simply the first column of ![]() – the first row of
– the first row of ![]() .
.
This direction of maximum stretch is again the solution to the variance-maximization problem (8). To see this, first plug in this choice ![]() to obtain
to obtain
![]()
Second, for every unit vector ![]() ,
, ![]() is also a unit vector (since
is also a unit vector (since ![]() is orthogonal), so
is orthogonal), so ![]() is an average of the
is an average of the ![]() ’s, just as in (11) (with averaging weights given by the squared coordinates of
’s, just as in (11) (with averaging weights given by the squared coordinates of ![]() , rather than those of
, rather than those of ![]() ). Thus
). Thus ![]() for every unit vector
for every unit vector ![]() , implying that
, implying that ![]() maximizes
maximizes ![]() .
.
2.1.5 General Covariance Matrices
We’ve seen that when the matrix ![]() can be written as
can be written as ![]() for an orthogonal matrix
for an orthogonal matrix ![]() and diagonal matrix
and diagonal matrix ![]() , it’s easy to understand how to maximize the variance in (8): the optimal solution is to set
, it’s easy to understand how to maximize the variance in (8): the optimal solution is to set ![]() equal to the first row of
equal to the first row of ![]() , and geometrically this is just the direction of maximum stretch when we view
, and geometrically this is just the direction of maximum stretch when we view ![]() as a map from
as a map from ![]() to itself called a linear operator. But we don’t want to solve the problem (8) only for diagonal matrices in disguise – we want to solve it for an arbitrary covariance matrix
to itself called a linear operator. But we don’t want to solve the problem (8) only for diagonal matrices in disguise – we want to solve it for an arbitrary covariance matrix ![]() . But wait, we’ve already done this: recall from linear algebra that every matrix
. But wait, we’ve already done this: recall from linear algebra that every matrix ![]() of the form
of the form ![]() can be written as
can be written as ![]() for an orthogonal matrix
for an orthogonal matrix ![]() and diagonal matrix
and diagonal matrix ![]() as in (10).
as in (10).
Recall from linear algebra that for some symmetric matrices ![]() , the corresponding diagonal matrix
, the corresponding diagonal matrix ![]() will have some negative entries. For symmetric matrices of the form
will have some negative entries. For symmetric matrices of the form ![]() , however, all of the diagonal entries are nonnegative. Such matrices are called “positive semindefinite”. To see this fact, note that
, however, all of the diagonal entries are nonnegative. Such matrices are called “positive semindefinite”. To see this fact, note that
- if
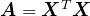 , then
, then 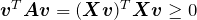 for every
for every 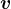
- if
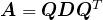 with the
with the 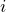 th diagonal entry of
th diagonal entry of 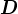 negative, then taking
negative, then taking 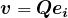 provides a vector with
provides a vector with 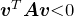 .
.
Now to summarize, so far we’ve shown the following:
When ![]() , the solution to (8) is the first row of
, the solution to (8) is the first row of ![]() , where
, where ![]() with
with ![]() orthonormal and
orthonormal and ![]() diagonal with sorted diagonal entries.
diagonal with sorted diagonal entries.
2.1.6 Solving for Larger Values of 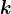
Solving for ![]() is no different than solving for
is no different than solving for ![]() . The solution to the variance-maximization problem in (7) is analogous, namely to pick the
. The solution to the variance-maximization problem in (7) is analogous, namely to pick the ![]() orthogonal axes that are stretched the most by
orthogonal axes that are stretched the most by ![]() . The extension to the derivation above gives the following generalization:
. The extension to the derivation above gives the following generalization:
For general ![]() , the solution to (7) is the first
, the solution to (7) is the first ![]() rows of
rows of ![]() , where
, where ![]() with
with ![]() orthonormal and
orthonormal and ![]() diagonal with sorted diagonal entries.
diagonal with sorted diagonal entries.
Note that since ![]() is orthonormal, the first
is orthonormal, the first ![]() rows of
rows of ![]() are indeed a set of
are indeed a set of ![]() orthonormal vectors, as required in (7). Note that, another way to arrive to the same
orthonormal vectors, as required in (7). Note that, another way to arrive to the same ![]() vectors is to choose
vectors is to choose ![]() as a the variance-maximizing direction (as in (8)); choose
as a the variance-maximizing direction (as in (8)); choose ![]() as the variance-maximizing direction orthogonal to
as the variance-maximizing direction orthogonal to ![]() ; choose
; choose ![]() as the variance-maximizing direction orthogonal to both
as the variance-maximizing direction orthogonal to both ![]() and
and ![]() ; and so on. For a matrix
; and so on. For a matrix ![]() , these are called the top
, these are called the top ![]() principal components of
principal components of ![]() .
.
2.1.7 Correlation with Eigenvectors and Eigenvalues
Now that we’ve characterized the top ![]() principal components as the first
principal components as the first ![]() rows of
rows of ![]() in the decomposition
in the decomposition ![]() , an obvious question arises: How do we compute them? And the answer to that question follows from the reinterpretation of these
, an obvious question arises: How do we compute them? And the answer to that question follows from the reinterpretation of these ![]() vectors as being the eigenvectors of the covarience matrix
vectors as being the eigenvectors of the covarience matrix ![]() .
.
Recall from linear algebra that an eigenvector of a matrix ![]() is a vector
is a vector ![]() that is stretched in the same direction by
that is stretched in the same direction by ![]() , meaning
, meaning ![]() for
for ![]() where the value
where the value ![]() is the corresponding eigenvalue. Eigenvectors are just the “axes of stretch” of the geometric discussions above, with eigenvalues giving the stretch factors.
is the corresponding eigenvalue. Eigenvectors are just the “axes of stretch” of the geometric discussions above, with eigenvalues giving the stretch factors.
When we write ![]() as
as ![]() , we’re actually writing the matrix in terms of its eigenvectors and eigenvalues – the rows of
, we’re actually writing the matrix in terms of its eigenvectors and eigenvalues – the rows of ![]() are the eigenvectors of
are the eigenvectors of ![]() , and the diagonal entries in
, and the diagonal entries in ![]() are the corresponding eigenvalues. To see this, consider the
are the corresponding eigenvalues. To see this, consider the ![]() th row of
th row of ![]() , which can be written
, which can be written ![]() . Since
. Since ![]() we have,
we have, ![]() . Hence the
. Hence the ![]() th row of
th row of ![]() is the eigenvector of A with eigenvalue
is the eigenvector of A with eigenvalue ![]() . Thus, the following sentence is often given as a definition of the PCA method:
. Thus, the following sentence is often given as a definition of the PCA method:
PCA boils down to computing the ![]() eigenvectors of the covariance matrix
eigenvectors of the covariance matrix ![]() that have the largest eigenvalues.
that have the largest eigenvalues.
Now that we’ve redefined the top ![]() principal components as being eigenvectors, one begins to wonder: are those top
principal components as being eigenvectors, one begins to wonder: are those top ![]() principal components of
principal components of ![]() uniquely defined? Well to answer this, we need to note that the set of diagonal entries in the matrix
uniquely defined? Well to answer this, we need to note that the set of diagonal entries in the matrix ![]() (the set of eigenvalues of
(the set of eigenvalues of ![]() ) is uniquely defined, since recall that we’re ordering the coordinates so that the entries are in a decreasing order. So:
) is uniquely defined, since recall that we’re ordering the coordinates so that the entries are in a decreasing order. So:
- If these eigenvalues are all distinct, then the matrix
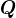 is also unique up to a sign flip in each column. Meaning if
is also unique up to a sign flip in each column. Meaning if 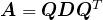 and
and 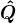 is
is 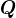 with all signs flipped in some column, then
with all signs flipped in some column, then 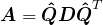 as well.
as well. - If an eigenvalues occurs with a multiplicity
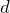 , then there is a
, then there is a 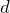 -dimensional subspace of corresponding eigenvectors. Thus, any orthogonal basis of this subspace can be chosen as the corresponding top
-dimensional subspace of corresponding eigenvectors. Thus, any orthogonal basis of this subspace can be chosen as the corresponding top 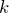 principal components.
principal components.
2.2 Using the Power Iteration Method
We first describe how to use the power iteration method to find the first eigenvector (which corresponds to the largest eigevalue), then explain how to use it to find the remaining ones.
2.2.1 The Algorithm
To understand the geometric intuition behind the method, recall that if one views the matrix ![]() as a function that maps the unit sphere to an ellipsoid, then the longest axis of the ellipsoid corresponds to the top eigenvector of
as a function that maps the unit sphere to an ellipsoid, then the longest axis of the ellipsoid corresponds to the top eigenvector of ![]() (see Figure 5 and Figure 6 for a visual representation). Given that the top eigenvector corresponds to the direction in which multiplication by
(see Figure 5 and Figure 6 for a visual representation). Given that the top eigenvector corresponds to the direction in which multiplication by ![]() stretches the vector the most, it is natural to hope that if we start with a random vector
stretches the vector the most, it is natural to hope that if we start with a random vector ![]() , and keep applying
, and keep applying ![]() over and over, then we will end up having stretched
over and over, then we will end up having stretched ![]() so much in the direction of
so much in the direction of ![]() ’s top eigenvector that the image of
’s top eigenvector that the image of ![]() will lie almost entirely in this same direction.
will lie almost entirely in this same direction.
For instance, in Figure 2, applying ![]() twice (rotate/stretch/rotate-back/rotate/stretch/rotate-back) will stretch the ellipsoid twice as far along the southwest-northeast direction (in the direction of the first eigenvector). Further applications of
twice (rotate/stretch/rotate-back/rotate/stretch/rotate-back) will stretch the ellipsoid twice as far along the southwest-northeast direction (in the direction of the first eigenvector). Further applications of ![]() will make this axis of stretch even more pronounced. Eventually, almost all of the points on the original unit circle get mapped to points that are very close to this axis as displayed in Figure 7 below .
will make this axis of stretch even more pronounced. Eventually, almost all of the points on the original unit circle get mapped to points that are very close to this axis as displayed in Figure 7 below .

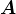 five times to the unit circle resulting with the dashed circle. Applying
five times to the unit circle resulting with the dashed circle. Applying 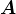 more times will align all points of the unit circle along the top eigenvector of
more times will align all points of the unit circle along the top eigenvector of 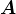 .
.The following is a formal statement of the power iteration method:
Algorithm 1 Power Iteration Given matrix:
Select random unit vector
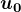
For
, set
. If
, then return
.
Do note that often one replaces the computation of ![]() and instead uses repeated squaring – to replace the larger number of matrix-vector multiplications with a smaller number of matrix-matrix multiplications – and computes
and instead uses repeated squaring – to replace the larger number of matrix-vector multiplications with a smaller number of matrix-matrix multiplications – and computes ![]() .
.
2.2.2 The Analysis
To show that the power iteration method works, we first prove that if ![]() then
then ![]() . Which means that
. Which means that ![]() has the same orientation (i.e. eigenvectors) as
has the same orientation (i.e. eigenvectors) as ![]() , but all the eigenvalues are raised to the power of
, but all the eigenvalues are raised to the power of ![]() (and hence are exaggerated). For example, if
(and hence are exaggerated). For example, if ![]() then
then ![]() .
.
Claim 1 If ![]() , then
, then ![]() .
.
Proof of Claim 1: We can prove this via induction on ![]() . The base case
. The base case ![]() is immediate. Now, assuming that the statement holds for
is immediate. Now, assuming that the statement holds for ![]() with
with ![]() , let’s check for
, let’s check for ![]() :
:
![]()
And thus, the induction step holds from the orthogonality of ![]() .
. ![]()
Now, we can quantify the performance of the power iteration algorithm using the following theorem:
Theorem 1 With probability of at least ![]() over the choice of
over the choice of ![]() and for
and for ![]() :
:
![]()
where ![]() is the top eigenvector of
is the top eigenvector of ![]() with eigenvalue
with eigenvalue ![]() and
and ![]() is the second-largest eigenvalue of
is the second-largest eigenvalue of ![]() .
.
This result shows that the number of iterations required scales as ![]() . The ratio
. The ratio ![]() is an important parameter called the spectral gap of the matrix
is an important parameter called the spectral gap of the matrix ![]() . The bigger the spectral gap, the more pronounced is the direction of maximum stretch (compared to other axes of stretch). If the spectral gap is large, then we are in excellent shape. If
. The bigger the spectral gap, the more pronounced is the direction of maximum stretch (compared to other axes of stretch). If the spectral gap is large, then we are in excellent shape. If ![]() , then the algorithm might take a long time (or might never) find
, then the algorithm might take a long time (or might never) find ![]() . If
. If ![]() , then
, then ![]() and
and ![]() are not uniquely defined – there is a two-dimensional subspace of eigenvectors with this eigenvalue. In this case, the power iteration algorithm will simply return a vector that lies in this subspace, which is the correct thing to do.
are not uniquely defined – there is a two-dimensional subspace of eigenvectors with this eigenvalue. In this case, the power iteration algorithm will simply return a vector that lies in this subspace, which is the correct thing to do.
For example, if ![]() then
then ![]() for any
for any ![]() , and so
, and so ![]() is essentially pointing in the same direction as
is essentially pointing in the same direction as ![]() .
.
The “with probability ![]() ” statement in Theorem 1 can be strengthened to “with probability at least
” statement in Theorem 1 can be strengthened to “with probability at least ![]() ” by repeating the above algorithm 100 times (for independent choices of
” by repeating the above algorithm 100 times (for independent choices of ![]() ), and outputting the recovered unit-length vector
), and outputting the recovered unit-length vector ![]() that maximizes
that maximizes ![]() .
.
Proof of Theorem 1: Let ![]() denote the eigenvectors of
denote the eigenvectors of ![]() , with associated eigenvalues
, with associated eigenvalues ![]() . These vectors form an orthonormal basis for
. These vectors form an orthonormal basis for ![]() . Write the random initial vector
. Write the random initial vector ![]() in terms of this basis. We claim that the probability at least
in terms of this basis. We claim that the probability at least ![]() ,
, ![]() . This follows straightforwardly from a computation, using the fact that we can choose a random unit vector by selecting each coordinate independently from a Gaussian of variance
. This follows straightforwardly from a computation, using the fact that we can choose a random unit vector by selecting each coordinate independently from a Gaussian of variance ![]() , and then normalizing (by a factor that will be very close to
, and then normalizing (by a factor that will be very close to ![]() ).
).
Given that ![]() , we have the following:
, we have the following:
![Rendered by QuickLaTeX.com \[ |\langle \frac{\boldsymbol{A}^t\boldsymbol{u_0}}{\|\boldsymbol{A}^t\boldsymbol{u_0}\|},\boldsymbol{v_1} \rangle|=\frac{c_1\lambda_1^t}{\sqrt{\sum_{i=1}^d{(\lambda_i^tc_i)^2}}}\geq\frac{c_1\lambda_1^t}{\sqrt{c^2\lambda_1^{2t}+d\lambda_2^{2t}}}\geq\frac{c_1\lambda_1^t}{c_1\lambda_1^t+\lambda_2^t\sqrt{d}}\geq1-2\sqrt{d}(\frac{\lambda_2}{\lambda_1})^t, \]](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-7b85e55edce092f68c3eebc190f22de2_l3.png)
where the second-to-last inequality follows from the fact that for any ![]() ,
, ![]() , and the last inequality follows from dividing the top and bottom by the numerator,
, and the last inequality follows from dividing the top and bottom by the numerator, ![]() , and noting that for
, and noting that for ![]() it holds that
it holds that ![]() .
. ![]()
2.2.3 Computing the Remaining Principal Components
Applying the power iteration algorithm to the covariance matrix ![]() of a data matrix
of a data matrix ![]() finds (a close approximation to) the top principal component of
finds (a close approximation to) the top principal component of ![]() . We can reuse the same method to compute subsequent principal components one-by-one, up to the desired number
. We can reuse the same method to compute subsequent principal components one-by-one, up to the desired number ![]() . Specifically, to find the top
. Specifically, to find the top ![]() principal components:
principal components:
- Find the top component,
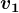 , using power iteration.
, using power iteration. - Project the data matrix orthogonally to
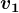 :
:
![Rendered by QuickLaTeX.com \[ \left[ {\begin{array}{ccc} \boldsymbol{-} & \boldsymbol{x_1} & \boldsymbol{-} \\ \boldsymbol{-} & \boldsymbol{x_2} & \boldsymbol{-} \\ & \vdots & \\ \boldsymbol{-} & \boldsymbol{x_n} & \boldsymbol{-} \end{array} } \right] \mapsto \left[ {\begin{array}{ccc} \boldsymbol{-} & (\boldsymbol{x_1} \boldsymbol{-} \langle \boldsymbol{x_1},\boldsymbol{v_1}\rangle \boldsymbol{v_1}) & \boldsymbol{-} \\ \boldsymbol{-} & (\boldsymbol{x_2} \boldsymbol{-} \langle \boldsymbol{x_1},\boldsymbol{v_1}\rangle \boldsymbol{v_1}) & \boldsymbol{-} \\ & \vdots & \\ \boldsymbol{-} & (\boldsymbol{x_n} \boldsymbol{-} \langle \boldsymbol{x_n},\boldsymbol{v_1}\rangle \boldsymbol{v_1}) & \boldsymbol{-} \end{array} } \right] .\]](https://blog.eliesaad.net/wp-content/ql-cache/quicklatex.com-4cc1efd5ff7fcfb93c90d081796385f4_l3.png)
This corresponds to subtracting out the variance of the data that is already explained by the first principal component ![]() .
.
- Recurse by finding the top
 principal components of the new data matrix.
principal components of the new data matrix.
The correctness of this greedy algorithm follows from the fact that the ![]() -dimensional subspace that maximizes the norms of the projections of a data matrix
-dimensional subspace that maximizes the norms of the projections of a data matrix ![]() contains the
contains the ![]() -dimensional subspace that maximizes the norms of the projections.
-dimensional subspace that maximizes the norms of the projections.
2.2.4 But How Does One Chooses 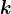 ?
?
How do you know how many principal components are “enough”? For data visualization, often you just want the first few. In other applications, like compression, the simple answer is that you don’t. In general, it is worth computing a lot of them and plotting their eigenvalues. Often the eigenvalues become small after a certain point – e.g., your data might have 200 dimensions, but after the first 50 eigenvalues, the rest are all tiny. Looking at this plot might give you some heuristic sense of how to choose the number of components so as to maximize the signal of your data, while preserving the low-dimensionality.
2.3 Using The Singular Value Decomposition Method
We have so far discussed in the previous section how to compute the top ![]() principal components using the Power Iteration Algorithm. The Power Iteration Method computes
principal components using the Power Iteration Algorithm. The Power Iteration Method computes ![]()
![]() -dimentional vectors
-dimentional vectors ![]() which are good approximations and are almost equal to the
which are good approximations and are almost equal to the ![]() eigenvectors with the associated top
eigenvectors with the associated top ![]() eigenvalues of the matrix
eigenvalues of the matrix ![]() which is a representation of a linear mapping from the vector space
which is a representation of a linear mapping from the vector space ![]() onto itself.
onto itself.
In this section we will focus on another algorithm called The Singular Value Decomposition (SVD). As we will see later on in this section, SVD expresses the matrix ![]() as a list of its ingredients, ordered by “importance”, from which we will only keep the
as a list of its ingredients, ordered by “importance”, from which we will only keep the ![]() most important ingredients.
most important ingredients.
2.3.1 The Definitions
We’ll start with the formal definitions, and then discuss interpretations, applications, and connections to the Power Iteration Method. A singular value decomposition (SVD) of an ![]() matrix
matrix ![]() expresses the matrix as the product of three “simple” matrices:
expresses the matrix as the product of three “simple” matrices:
(8) ![]()
where:
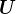 is an
is an 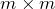 orthogonal matrix;
orthogonal matrix; is an
is an 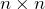 orthogonal matrix;
orthogonal matrix;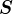 is an
is an 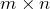 diagonal matrix with nonnegative entries, and with the diagonal entries sorted from high to low.
diagonal matrix with nonnegative entries, and with the diagonal entries sorted from high to low.
Note that in contrast to the decomposition discussed in section 2 – up until this SVD part – (![]() when
when ![]() has the form
has the form ![]() ), the orthogonal matrices
), the orthogonal matrices ![]() and
and ![]() are not the same – since
are not the same – since ![]() need not be square,
need not be square, ![]() and
and ![]() need not even have the same dimensions. Do note that, even small numerical examples are tedious to do in detail – the orthogonality constraint on singular vectors ensures that most of the numbers are messy. The easiest way to get a feel for what SVDs look like is to feed a few small matrices into the SVD subroutine supported by your favorite environment (Matlab, python’s numpy library, etc).
need not even have the same dimensions. Do note that, even small numerical examples are tedious to do in detail – the orthogonality constraint on singular vectors ensures that most of the numbers are messy. The easiest way to get a feel for what SVDs look like is to feed a few small matrices into the SVD subroutine supported by your favorite environment (Matlab, python’s numpy library, etc).
The columns of ![]() are called the left singular vectors of
are called the left singular vectors of ![]() (these are
(these are ![]() -vectors). The columns of
-vectors). The columns of ![]() (that is, the rows of
(that is, the rows of ![]() ) are the right singular vectors of
) are the right singular vectors of ![]() (these are
(these are ![]() -vectors). The entries of
-vectors). The entries of ![]() are the singular values of
are the singular values of ![]() . Thus with each singular vector (left or right) there is an associated singular value. The “first” or “top” singular vector refers to the one associated with the largest singular value, and so on. As visually shown in Figure 8 below.
. Thus with each singular vector (left or right) there is an associated singular value. The “first” or “top” singular vector refers to the one associated with the largest singular value, and so on. As visually shown in Figure 8 below.

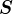 has an associated left singular vector in
has an associated left singular vector in 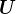 , and right singular vector in
, and right singular vector in  .
.To better see how the SVD expresses ![]() as a “list of its ingredients”, check that the factorization
as a “list of its ingredients”, check that the factorization ![]() is equivalent to the expression
is equivalent to the expression
(9) 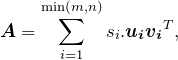
where ![]() is the
is the ![]() th singular value and
th singular value and ![]() ,
, ![]() are the corresponding left and right singular vectors. That is, the SVD expresses
are the corresponding left and right singular vectors. That is, the SVD expresses ![]() as a nonnegative linear combination of
as a nonnegative linear combination of ![]() rank-1 matrices, with the singular values providing the multipliers and the outer products of the left and right singular vectors providing the rank-1 matrices.
rank-1 matrices, with the singular values providing the multipliers and the outer products of the left and right singular vectors providing the rank-1 matrices.
Every matrix A has a SVD. The proof is not deep, but is better covered in a linear algebra course than here. Geometrically, thinking of an ![]() matrix as a mapping from
matrix as a mapping from ![]() to
to ![]() , this fact is kind of amazing: every matrix
, this fact is kind of amazing: every matrix ![]() , no matter how weird, is only performing a rotation in the domain (multiplication by
, no matter how weird, is only performing a rotation in the domain (multiplication by ![]() ), followed by scaling plus adding or deleting dimensions (multiplication by
), followed by scaling plus adding or deleting dimensions (multiplication by ![]() ) as needed, followed by a rotation in the range (multiplication by
) as needed, followed by a rotation in the range (multiplication by ![]() ). Along the lines of last section’s discussion, the SVD is “more or less unique”. The singular values of a matrix are unique. When a singular value appears multiple times, the subspaces spanned by the corresponding left and right singular vectors are uniquely defined, but arbitrary orthonormal bases can be chosen for each. Also, do note that one can always multiply the
). Along the lines of last section’s discussion, the SVD is “more or less unique”. The singular values of a matrix are unique. When a singular value appears multiple times, the subspaces spanned by the corresponding left and right singular vectors are uniquely defined, but arbitrary orthonormal bases can be chosen for each. Also, do note that one can always multiply the ![]() th left and right singular vectors by
th left and right singular vectors by ![]() to get another SVD.
to get another SVD.
2.3.2 Methods of Computing the SVD
There are pretty good algorithms for computing the SVD of a matrix, details are covered in any numerical analysis course. One simple method worthy of being mentioned consists of finding the eigenvalues and eigenvectors of ![]() and
and ![]() to calculate the SVD of
to calculate the SVD of ![]() . The eigenvectors of
. The eigenvectors of ![]() make up the columns of
make up the columns of ![]() , the eigenvectors of
, the eigenvectors of ![]() make up the columns of
make up the columns of ![]() . Also, the singular values in
. Also, the singular values in ![]() are square roots of eigenvalues from
are square roots of eigenvalues from ![]() or
or ![]() . The singular values are the diagonal entries of the
. The singular values are the diagonal entries of the ![]() matrix and are arranged in descending order (as mentioned before). The singular values are always real numbers. If the matrix
matrix and are arranged in descending order (as mentioned before). The singular values are always real numbers. If the matrix ![]() is a real matrix, then
is a real matrix, then ![]() and
and ![]() are also real. The details of this method are further explained later on in this section.
are also real. The details of this method are further explained later on in this section.
2.3.3 Low-Rank Approximations from the SVD
Recalling that the SVD expresses a matrix A as a sum of rank-![]() matrices (weighted by the corresponding singular values), a natural idea is to keep only the first k terms on the right-hand side of (15). That is, for
matrices (weighted by the corresponding singular values), a natural idea is to keep only the first k terms on the right-hand side of (15). That is, for ![]() as in (15) and a target rank
as in (15) and a target rank ![]() , the proposed rank-
, the proposed rank-![]() approximation is
approximation is
(10) 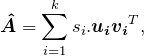
where as usual we assume that the singular values have been sorted (![]() ), and
), and ![]() and
and ![]() denote the
denote the ![]() th left and right singular vectors. As the sum of
th left and right singular vectors. As the sum of ![]() rank-
rank-![]() matrices,
matrices, ![]() clearly has rank (at most)
clearly has rank (at most) ![]() .
.
Here is an equivalent way to think about the proposed rank-![]() approximation (see also Figure 9 below).
approximation (see also Figure 9 below).

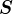 is non-zero only on its diagonal, and the diagonal entries of
is non-zero only on its diagonal, and the diagonal entries of 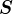 are sorted from high to low. Our low rank approximation is
are sorted from high to low. Our low rank approximation is 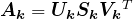 .
. - Compute the SVD
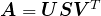 , where
, where 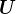 is an
is an 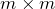 orthogonal matrix,
orthogonal matrix, 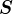 is a nonnegative
is a nonnegative 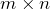 diagonal matrix with diagonal entries sorted from high to low, and
diagonal matrix with diagonal entries sorted from high to low, and 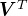 is a
is a 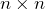 orthogonal matrix.
orthogonal matrix. - Keep only the top
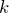 right singular vectors: set
right singular vectors: set 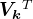 equal to the first
equal to the first 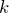 rows of
rows of 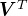 (a
(a 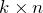 matrix).
matrix). - Keep only the top
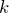 left singular vectors: set
left singular vectors: set 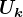 equal to the first
equal to the first 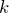 columns of
columns of 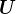 (an
(an 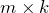 matrix).
matrix). - Keep only the top
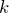 singular values: set
singular values: set 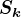 equal to the first
equal to the first 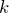 rows and columns of
rows and columns of 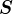 (a
(a 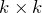 matrix), corresponding to the
matrix), corresponding to the 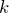 largest singular values of
largest singular values of 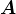 .
. - The rank-
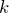 approximation is then
approximation is then
(11) ![]()
Storing the matrices on the right-hand side of (17) takes ![]() space, in contrast to the
space, in contrast to the ![]() space required to store the original matrix
space required to store the original matrix ![]() . This is a big win when
. This is a big win when ![]() is relatively small and
is relatively small and ![]() and
and ![]() are relatively large (as in many applications).
are relatively large (as in many applications).
It is natural to interpret (17) as approximating the raw data ![]() in terms of
in terms of ![]() “concepts” (e.g. “math”, “music”, and “sports”), where the singular values of
“concepts” (e.g. “math”, “music”, and “sports”), where the singular values of ![]() express the signal strengths of these concepts, the rows of
express the signal strengths of these concepts, the rows of ![]() and columns of
and columns of ![]() express the “canonical row/column” associated with each concept (e.g. a customer that likes only music products, or a product liked only by music customers), and the rows of
express the “canonical row/column” associated with each concept (e.g. a customer that likes only music products, or a product liked only by music customers), and the rows of ![]() (respectively, columns of
(respectively, columns of ![]() ) approximately express each row (respectively, column) of
) approximately express each row (respectively, column) of ![]() as a linear combination (scaled by
as a linear combination (scaled by ![]() ) of the “canonical rows” (respectively, canonical columns).
) of the “canonical rows” (respectively, canonical columns).
Conceptually, this method of producing a low-rank approximation is as clean as could be imagined: we re-represent ![]() using the SVD, which provides a list of
using the SVD, which provides a list of ![]() ’s “ingredients,” ordered by “importance”, and we retain only the
’s “ingredients,” ordered by “importance”, and we retain only the ![]() most important ingredients. But is the result of this elegant computation any good?
most important ingredients. But is the result of this elegant computation any good?
The next fact justifies this approach: this low-rank approximation is optimal in a natural sense. The guarantee is in terms of the “Frobenius norm” of a matrix ![]() , which just means applying the
, which just means applying the ![]() norm to the matrix as if it were a vector:
norm to the matrix as if it were a vector: ![]() .
.
Fact 1 For every ![]() matrix
matrix ![]() , rank target
, rank target ![]() , and rank-
, and rank-![]()
![]() matrix
matrix ![]() ,
,
![]()
where ![]() is the rank-
is the rank-![]() approximation (17) derived from the SVD of
approximation (17) derived from the SVD of ![]() .
.
We won’t prove Fact 1 formally, but see the previous section for a plausibility argument based on the properties we’ve already established about the closely related PCA method.
2.3.4 How to Choose 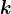
When producing a low-rank matrix approximation, we’ve been taking as a parameter the target rank k. But how should ![]() be chosen? In a perfect world, the singular values of
be chosen? In a perfect world, the singular values of ![]() give strong guidance: if the top few such values are big and the rest are small, then the obvious solution is to take
give strong guidance: if the top few such values are big and the rest are small, then the obvious solution is to take ![]() equal to the number of big values. In a less perfect world, one takes
equal to the number of big values. In a less perfect world, one takes ![]() as small as possible subject to obtaining a useful approximation – of course what “useful” means depends on the application. Rules of thumb often take the form: choose
as small as possible subject to obtaining a useful approximation – of course what “useful” means depends on the application. Rules of thumb often take the form: choose ![]() such that the sum of the top
such that the sum of the top ![]() singular values is at least
singular values is at least ![]() times as big as the sum of the other singular values, where
times as big as the sum of the other singular values, where ![]() is a domain-dependent constant (like
is a domain-dependent constant (like ![]() , say).
, say).
2.3.5 Lossy Compression via Truncated Decomposition
Using the SVD to produce low-rank matrix approximations is another example of a useful paradigm for lossy compression. The first step of the paradigm is to re-express the raw data exactly as a decomposition into several terms (as in (14)). The second step is to throw away all but the “most important” terms, yielding an approximation of the original data. This paradigm works well when you can find a representation of the data such that most of the interesting information is concentrated in just a few components of the decomposition. The appropriate representation will depend on the data set – though there are a few rules of thumb, as we’ll discuss – and of course, messy enough data sets might not admit any nice representations at all.
2.3.6 PCA Reduces to SVD
There is an interesting relationship between the SVD and the decompositions we discussed in the last section. Recall that we used the fact that ![]() , as a symmetric
, as a symmetric ![]() matrix, can be written as
matrix, can be written as ![]() , where
, where ![]() is an
is an ![]() orthogonal matrix and
orthogonal matrix and ![]() is an
is an ![]() diagonal matrix. (Here
diagonal matrix. (Here ![]() is the data matrix, with each of the
is the data matrix, with each of the ![]() rows representing a data point in
rows representing a data point in ![]() ). Consider the SVD
). Consider the SVD ![]() and what its existence means for
and what its existence means for ![]() :
:
(12) ![]()
where ![]() is a diagonal matrix with diagonal entries equal to the squares of the diagonal entries of
is a diagonal matrix with diagonal entries equal to the squares of the diagonal entries of ![]() (if
(if ![]() then the remaining
then the remaining ![]() diagonal entries of
diagonal entries of ![]() are 0).
are 0).
Recall from last lecture that if we decompose ![]() as
as ![]() , then the rows of
, then the rows of ![]() are the eigenvectors of
are the eigenvectors of ![]() . The computation in (18) therefore shows that the rows of
. The computation in (18) therefore shows that the rows of ![]() are the eigenvectors of
are the eigenvectors of ![]() . Thus, the right singular vectors of
. Thus, the right singular vectors of ![]() are the same as the eigenvectors of
are the same as the eigenvectors of ![]() . Similarly, the eigenvalues of
. Similarly, the eigenvalues of ![]() are the squares of the singular values of
are the squares of the singular values of ![]() .
.
Thus PCA reduces to computing the SVD of ![]() (without forming
(without forming ![]() ). Recall that the output of PCA, given a target
). Recall that the output of PCA, given a target ![]() , is simply the top
, is simply the top ![]() eigenvectors of the covariance matrix
eigenvectors of the covariance matrix ![]() . The SVD
. The SVD ![]() of
of ![]() hands you these eigenvectors on a silver platter they are simply the first
hands you these eigenvectors on a silver platter they are simply the first ![]() rows of
rows of ![]() . This is an alternative to the Power Iteration method discussed in the previous section. So which method for computing eigenvectors is better? There is no clear answer; in many cases, either should work fine, and if performance is critical you’ll want to experiment with both. Certainly the Power Iteration method, which finds the eigenvectors of
. This is an alternative to the Power Iteration method discussed in the previous section. So which method for computing eigenvectors is better? There is no clear answer; in many cases, either should work fine, and if performance is critical you’ll want to experiment with both. Certainly the Power Iteration method, which finds the eigenvectors of ![]() one-by-one, looks like a good idea when you only want the top few eigenvectors (as in our data visualization use cases). If you want many or all of them, then the SVD – which gives you all of the eigenvectors, whether you want them or not – is probably the first thing to try.
one-by-one, looks like a good idea when you only want the top few eigenvectors (as in our data visualization use cases). If you want many or all of them, then the SVD – which gives you all of the eigenvectors, whether you want them or not – is probably the first thing to try.
Now that we understand the close connection between the SVD and the PCA method, let’s return to Fact 1, which states that the SVD-based rank-![]() approximation is optimal (with respect to the Frobenius norm). Intuitively, this fact holds because: (i) minimizing the Frobenius norm
approximation is optimal (with respect to the Frobenius norm). Intuitively, this fact holds because: (i) minimizing the Frobenius norm ![]() is equivalent to minimizing the average (over i) of the squared Euclidean distances between the
is equivalent to minimizing the average (over i) of the squared Euclidean distances between the ![]() th rows of
th rows of ![]() and
and ![]() ; (ii) the SVD uses the same vectors to approximate the rows of
; (ii) the SVD uses the same vectors to approximate the rows of ![]() as PCA (the top eigenvectors of
as PCA (the top eigenvectors of ![]() /right singular vectors of
/right singular vectors of ![]() ); and (iii) PCA, by definition, chooses its
); and (iii) PCA, by definition, chooses its ![]() vectors to minimize the average squared Euclidean distance between the rows of
vectors to minimize the average squared Euclidean distance between the rows of ![]() and the
and the ![]() -dimensional subspace of linear combinations of these vectors. The contribution of a row of
-dimensional subspace of linear combinations of these vectors. The contribution of a row of ![]() to the Frobenius norm corresponds exactly to one of these squared Euclidean distances.
to the Frobenius norm corresponds exactly to one of these squared Euclidean distances.
2.3.7 More on PCA vs. SVD
PCA and SVD are closely related, and in data analysis circles you should be ready for the terms to be used almost interchangeably. There are differences, however. First, PCA refers to a data analysis approach – a choice of how to define the “best” way to approximate a bunch of data points as linear combinations of a small set of vectors. Meanwhile, the SVD is a general operation defined on all matrices. For example, it doesn’t really make sense to talk about “applying PCA” to a matrix ![]() unless the rows of
unless the rows of ![]() have clear semantics – typically, as data points
have clear semantics – typically, as data points ![]() . By contrast, the SVD (14) is well defined for every matrix
. By contrast, the SVD (14) is well defined for every matrix ![]() , whatever the semantics for
, whatever the semantics for ![]() . In the particular case where
. In the particular case where ![]() is a matrix where the rows represent data points, the SVD can be interpreted as performing the calculations required by PCA (The SVD is also useful for many other computational tasks).
is a matrix where the rows represent data points, the SVD can be interpreted as performing the calculations required by PCA (The SVD is also useful for many other computational tasks).
We can also make more of an “apples vs. apples” comparison in the following way. Let’s define the “PCA operation” as taking an ![]() data matrix
data matrix ![]() as input, and possibly a parameter
as input, and possibly a parameter ![]() , and outputting all (or the top
, and outputting all (or the top ![]() ) eigenvectors of the covariance matrix
) eigenvectors of the covariance matrix ![]() . The “SVD operation” takes as input an
. The “SVD operation” takes as input an ![]() matrix
matrix ![]() and outputs
and outputs ![]() ,
, ![]() , and
, and ![]() , where the rows of
, where the rows of ![]() are the eigenvectors of
are the eigenvectors of ![]() . Thus the SVD gives strictly more information than required by PCA, namely the matrix
. Thus the SVD gives strictly more information than required by PCA, namely the matrix ![]() .
.
Is the additional information ![]() provided by the SVD useful? In applications where you want to understand the column structure of
provided by the SVD useful? In applications where you want to understand the column structure of ![]() , in addition to the row structure, the answer is “yes.” To see this, let’s review some interpretations of the SVD (14). On the one hand, the decomposition expresses every row of
, in addition to the row structure, the answer is “yes.” To see this, let’s review some interpretations of the SVD (14). On the one hand, the decomposition expresses every row of ![]() as a linear combinations of the rows of
as a linear combinations of the rows of ![]() , with the rows of
, with the rows of ![]() providing the coefficients of these linear combinations. That is, we can interpret the rows of
providing the coefficients of these linear combinations. That is, we can interpret the rows of ![]() in terms of the rows of
in terms of the rows of ![]() , which is useful when the rows of
, which is useful when the rows of ![]() have interesting semantics. Analogously, the decomposition in (14) expresses the columns of
have interesting semantics. Analogously, the decomposition in (14) expresses the columns of ![]() as linear combinations of the columns of
as linear combinations of the columns of ![]() , with the coefficients given by the columns of
, with the coefficients given by the columns of ![]() . So when the columns of
. So when the columns of ![]() are interpretable, the decomposition gives us a way to understand the columns of
are interpretable, the decomposition gives us a way to understand the columns of ![]() .
.
In some applications, we really only care about understanding the rows of ![]() , and the extra information
, and the extra information ![]() provided by the SVD over PCA is irrelevant. In other applications, both the rows and the columns of
provided by the SVD over PCA is irrelevant. In other applications, both the rows and the columns of ![]() are interesting in their own right. For example:
are interesting in their own right. For example:
- Suppose rows of
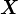 are indexed by customers, and the columns by products, with the matrix entries indicating who likes what. We are interested in understanding the rows, and in the best-case scenario, the right singular vectors (rows of
are indexed by customers, and the columns by products, with the matrix entries indicating who likes what. We are interested in understanding the rows, and in the best-case scenario, the right singular vectors (rows of 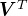 ) are interpretable as “customer types” or “canonical customers” and the SVD expresses each customer as a mixture of customer types. For example, perhaps each student’s purchasing history can be understood simply as a mixture of a “CS customer,” a “music customer”, and a “clothing customer.” In the ideal case, the left singular vectors (columns of
) are interpretable as “customer types” or “canonical customers” and the SVD expresses each customer as a mixture of customer types. For example, perhaps each student’s purchasing history can be understood simply as a mixture of a “CS customer,” a “music customer”, and a “clothing customer.” In the ideal case, the left singular vectors (columns of 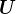 ) can be interpreted as “product types”, where the “types” are the same as for customers, and the SVD expresses each product as a mixture of product types (the extent to which a product appeals to a “CS customer”, a “music customer”, etc).
) can be interpreted as “product types”, where the “types” are the same as for customers, and the SVD expresses each product as a mixture of product types (the extent to which a product appeals to a “CS customer”, a “music customer”, etc). - Suppose the matrix represents data about drug interactions, with the rows of
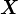 indexed by proteins or pathways, and the columns by chemicals or drugs. We’re interested in understanding both proteins and drugs in their own right, as mixtures of a small set of “basic types.”
indexed by proteins or pathways, and the columns by chemicals or drugs. We’re interested in understanding both proteins and drugs in their own right, as mixtures of a small set of “basic types.”
In the above two examples, what we really care about is the relationships between two groups of objects – customers and products, or proteins and drugs – the labeling of one group as the “rows” of a matrix and the other as the “columns” is arbitrary. In such cases, you should immediately think of the SVD as a potential tool for better understanding the data. When the columns of ![]() are not interesting in their own right, PCA already provides the relevant information.
are not interesting in their own right, PCA already provides the relevant information.
. . .
This concludes the second chapter in this series which deeply tackled the mathematics behind the Power Iteration and the SVD methods for computing the principal component vectors for PCA. In the next post we’ll apply everything we’ve learned in this post to make a face recognition model using the PCA method. We’ll apply the model (which uses PCA and SVM) using Python, so a basic understanding of code writing is required for this next chapter. Do note that unlike PCA, SVM is a classification algorithm which we will discuss in another post.
